密码实验
仿射密码
1 | from math import gcd |
解释
好的,我们来详细讲解一下 仿射密码 及你贴出来的这段 Python 代码,帮你理解它的原理和实现。
🔐 一、什么是仿射密码(Affine Cipher)?
仿射密码是一种古典加密算法,属于单字母替换密码的范畴。它结合了两个数学变换:
- 线性变换(乘法+加法)
- 模运算(取余)
加密公式:
对每个明文字母用以下公式变换:
[
E(x) = (a \cdot x + b) \mod 26
]
- ( x ):明文字母在字母表中的位置(0~25)
- ( a, b ):密钥参数
- ( \mod 26 ):因为英文字母有26个,所以对26取余
解密公式:
[
D(y) = a^{-1} \cdot (y - b) \mod 26
]
- ( y ):密文字母在字母表中的位置
- ( a^{-1} ):模 26 下的 ( a ) 的乘法逆元(即满足 ( a \cdot a^{-1} \equiv 1 \mod 26 ) 的整数)
注意:只有当 ( \gcd(a, 26) = 1 ) 时,乘法逆元 ( a^{-1} ) 才存在,所以 a 必须与 26 互质。
🧠 二、代码逐步解释
1. text_to_numbers(text)
1 | def text_to_numbers(text): |
功能: 把文本转换为字母在字母表中的数字(a=0, b=1, …, z=25)
例子:text_to_numbers("abc") 输出 [0, 1, 2]
2. encryption(m, a, b)
1 | def encryption(m, a, b): |
功能:使用仿射加密公式加密明文
- 先把明文变成数字列表
- 然后用
(a*x + b) % 26加密 - 最后把加密后的数字变回字母,拼接输出
3. decryption(c, a, b)
1 | def decryption(c, a, b): |
功能:仿射解密
- 先求出 ( a^{-1} )
- 然后用解密公式解密
(a_inv * (y - b)) % 26 - 最后还原成明文输出
4. get_valid_key_a()
1 | def get_valid_key_a(): |
功能:确保用户输入的 a 合法,即与 26 互质。
5. main()
1 | def main(): |
功能:主程序入口
- 用户选择加密或解密
- 然后输入明文或密文及密钥
- 调用加密或解密函数
🧪 三、实验操作步骤总结
- 打开 Python 开发环境(如 IDLE、PyCharm 或终端)
- 粘贴并运行上述代码
- 根据提示输入:
- 明文或密文
- 合法的
a(与26互质,比如 1, 3, 5, 7, 11…) - 任意整数
b
- 查看输出的加密或解密结果
✅ 四、实验结果示例
输入:
1 | 请选择操作:1 |
输出:
1 | 加密后的密文是:rclla |
然后用相同的 a 和 b 解密:1
2
3
4请选择操作:2
请输入密文:rclla
请输入密钥a:5
请输入密钥b:8
输出:1
解密后的明文是:hello
💡 五、实验心得
- 仿射密码是理解更复杂密码算法的基础。
- 通过手动编码加密/解密过程,可以加深对模运算和逆元的理解。
- 加密算法不仅要保证加密效果,还必须保证可以还原,即“可逆性”。
- Python 的
pow(a, -1, m)很方便地找到了乘法逆元,不需要手写扩展欧几里得算法。
如果你还想要:
- 图解加密过程
- 可视化步骤
- 支持大写字母或空格
我也可以帮你扩展这个程序!要不要来个 GUI 版本的?😄
DES
1 |
|
以下是关于DES加密算法及其代码实现的详细解析:
一、DES算法流程解析
初始置换(IP置换)
输入:64位明文
处理:根据IP表进行位置置换(原第58位成为新第1位,第50位成为新第2位…)
输出:置换后的64位数据分为L₀(前32位)和R₀(后32位)16轮Feistel结构
每轮处理流程:
好问题!DES(数据加密标准)最核心的一步之一就是子密钥的生成,也叫密钥调度(Key Schedule)。我们一步步来讲,保证你这个密码小白也能听懂😎
🧩 一、子密钥是啥?有什么用?
- DES 是一个 对称加密算法,用了 16 轮 Feistel 结构。
- 每一轮都要用一个 不同的子密钥(共 16 个子密钥)。
- 主密钥是 64 位(但只用其中的 56 位),从它生成 16 个 48 位的子密钥。
- 每轮加密/解密时,都从这 16 个子密钥中取对应的一个用。
✅ 子密钥的作用:
每轮加密都要和子密钥做异或、S盒替换等操作,不同子密钥让每轮加密都不同,增强了安全性。
🔑 二、怎么从主密钥生成子密钥?
Step 1️⃣:64位主密钥 → 56位有效密钥(去除奇偶校验位)
主密钥长这样(64 位):
1 | K = k1 k2 k3 ... k64 |
每 8 位中第 8 位是奇偶校验位(也就是说每 8 位只用前 7 位),所以有效密钥是 56 位。
这一步用的是一个固定的 PC-1(Permuted Choice 1)置换表,对密钥进行置换和选择,去掉了校验位。
Step 2️⃣:将 56 位密钥分成两半
1 | C0 = 前 28 位 |
Step 3️⃣:循环左移 + PC-2 生成 16 个子密钥
从 C0 和 D0 开始,每一轮做 左移(1 位或 2 位,按轮数):
| 轮数 | 移位次数 |
|---|---|
| 1, 2, 9, 16 | 1 位 |
| 其他轮 | 2 位 |
每轮都得到了:
1 | C1, D1 → K1 |
每次将 Cn 和 Dn 合并成 56 位,然后再用一个固定的 PC-2 表(Permuted Choice 2) 提取其中的 48 位生成 子密钥 Kn。
✏️ 小结
| 步骤 | 内容 |
|---|---|
| PC-1 | 把 64 位主密钥变成 56 位(去奇偶位) |
| 分割 | 56 位 → C0 和 D0,各 28 位 |
| 左移 | 每轮对 C 和 D 循环左移 1 或 2 位 |
| PC-2 | 从 CnDn 中选出 48 位 → 生成第 n 轮子密钥 |
🛠 子密钥在加密中的使用
在 DES 的每一轮加密中:
- 将明文左右分成 L 和 R。
- 用右边部分和当前轮的 子密钥 做复杂函数
f(R, K_i),包括:- 扩展置换
- 和子密钥异或
- S盒替换
- P盒置换
- 结果再和左边部分异或
- 左右换位进入下一轮
🚀 总结一句话:
子密钥是从主密钥中衍生出来的一组 48 位密钥,用于 DES 的每一轮加密。它通过置换、分割、循环移位、再次置换来生成,确保每一轮操作不同,增强安全性。
如果你想,我可以给你画一张 子密钥生成流程图,或者写一段 Python 实现 DES 密钥调度的代码~需要吗?
(1) 右半部分Rₙ进行扩展置换E(32→48位)
(2) 与子密钥Kₙ进行异或运算
(3) 通过8个S盒进行非线性变换(48→32位)
(4) 进行P盒置换
(5) 结果与左半部分Lₙ异或生成新右半部分Rₙ₊₁
(6) 交换左右部分
- 逆初始置换(IP⁻¹置换)
输入:最终合并的R₁₆L₁₆(注意不交换)
处理:根据IP_INV表进行置换
输出:64位密文
二、代码模块解析
- 置换表定义
代码中定义了DES算法所需的所有置换表:
- IP/IP_INV:初始/逆初始置换
- PC1/PC2:密钥置换表
- E:扩展置换表
- S_BOX:非线性替换盒
- P:P盒置换表
- SHIFT:循环左移位数表
- 核心函数说明
(1)permute(bits, table)功能:通用置换函数1
2def permute(bits, table):
return ''.join([bits[i - 1] for i in table])
特点:处理所有DES置换操作,自动处理索引偏移(表格定义从1开始,Python索引从0开始)
(2)generate_subkeys(key)1
2
3
4
5
6
7
8
9
10
11def generate_subkeys(key):
key = permute(key, PC1) # PC-1置换
left, right = key[:28], key[28:] # 分割
subkeys = []
for i in range(16):
left = left_shift(left, SHIFT[i]) # 循环左移
right = left_shift(right, SHIFT[i])
combined = left + right
subkey = permute(combined, PC2) # PC-2置换
subkeys.append(subkey)
return subkeys
功能:生成16轮子密钥
流程:
- 64位密钥→PC1置换→56位
- 分割为左右28位
- 根据SHIFT表进行循环左移
- 合并后通过PC2置换生成48位子密钥
(3)feistel(right, subkey)1
2
3
4
5
6
7
8
9
10
11
12def feistel(right, subkey):
expanded = permute(right, E) # 扩展置换
xored = xor(expanded, subkey) # 异或运算
s_output = ''
for i in range(8): # S盒处理
chunk = xored[i*6:(i+1)*6]
row = int(chunk[0]+chunk[5], 2) # 行号
col = int(chunk[1:5], 2) # 列号
val = S_BOX[i][row][col]
s_output += bin(val)[2:].zfill(4)
p_output = permute(s_output, P) # P盒置换
return p_output
功能:实现Feistel网络的核心变换
特点:
- 扩展置换使32位→48位
- 每个S盒处理6位→4位
- 最终通过P盒增强扩散性
你的代码里feistel函数用到了 S盒(Substitution Box),这是 DES 加密中的一大核心!我们来详细拆解一下 S 盒的逻辑和作用,让你从密码小白变成密码达人 🚀
🔐 一、S盒是干嘛的?
S盒的作用是:
把 6 位二进制输入,替换成 4 位输出。
它引入了 非线性变换,是 DES 安全性的重要来源之一。
📦 二、S盒是怎么操作的?
输入:6 位二进制(比如 011011)
步骤:
取第 1 位和第 6 位,拼起来当作 行号
1
row = int(chunk[0] + chunk[5], 2) # 例如 "01" → 1
取中间 4 位(第 2~5 位)当作 列号
1
col = int(chunk[1:5], 2) # 例如 "1101" → 13
查 S_BOX 中第 i 个盒子的第 row 行第 col 列的值
1
val = S_BOX[i][row][col] # 得到 0~15 之间的整数
把这个值转为 4 位二进制,作为输出:
1
s_output += bin(val)[2:].zfill(4)
🧪 举个例子:
假设 chunk = "011011",这是第 i 个块:
row = int("01", 2) = 1col = int("1101", 2) = 13val = S_BOX[i][1][13]→ 可能是 10bin(10)[2:].zfill(4)→"1010"
这样 6 位输入变成 4 位输出。
🔁 三、为什么一共是 8 个 S盒?
因为 DES 中的 Feistel 函数处理的是 32 位数据,但:
- 扩展置换 E 把 32 位 → 48 位
- 然后每 6 位为一组,分成 8 组
- 每组走一个 S 盒 → 输出 4 位
- 8 组共输出 32 位
这就实现了 48 位 → 32 位 的非线性压缩映射!
🔒 四、S盒的安全性来源
S盒是 DES 安全性的关键所在,因为它:
- 提供非线性映射,使得密文对密钥和明文的小改动非常敏感(雪崩效应)
- 是抗差分分析、线性分析等密码攻击的核心防线
- 是人工设计 + 安全性评估过的(是当年 NSA 优化过的)
✅ 总结一句话:
S盒就是一种查表替换机制:每 6 位输入 → 找行列 → 输出 4 位,8 个 S盒并行处理,共输出 32 位,用于混淆原始数据,增强加密的复杂性和安全性。
(4)des(block, key, encrypt=True)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17def des(block, key, encrypt=True):
subkeys = generate_subkeys(key)
if not encrypt:
subkeys = subkeys[::-1] # 解密时逆序密钥
block = permute(block, IP) # 初始置换
left, right = block[:32], block[32:]
for i in range(16): # 16轮迭代
new_left = right
f_result = feistel(right, subkeys[i])
new_right = xor(left, f_result)
left, right = new_left, new_right
combined = right + left # 最终不交换
ciphertext = permute(combined, IP_INV)
return ciphertext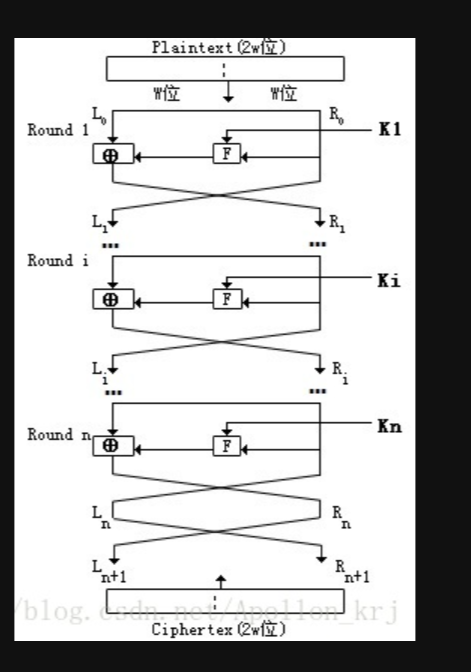
特点:
- 通过encrypt参数控制加密/解密模式
- 16轮迭代后不交换左右部分
- 最终执行逆初始置换
三、测试用例解析
弱密钥测试
1
2
3
4
5
6# 测试用例1:弱密钥
plaintext = 'aaabbaba' # ASCII明文
key = '0101010101010101' # 全01交替的弱密钥
# 加密结果:B4B15AFCB6A8F4C5
# 二次加密结果恢复原文现象说明:弱密钥的对称性导致二次加密恢复原文,这是DES密钥空间中的特殊现象。
半弱密钥测试
1
2
3
4
5# 半弱密钥测试
key1 = '011f011f010e010e'
key2 = '1f011f010e010e01'
# 使用key1加密后再用key2加密,等价于单次加密现象说明:半弱密钥对(K1,K2)满足E(K1,E(K2,M))=M,这种密钥对在DES密钥空间中存在特定数学关系。
四、代码特点分析
- 二进制处理
- 所有数据内部以二进制字符串形式处理
- 提供text_to_bin()处理十六进制/ASCII输入
- bin_to_hex()用于结果输出
- 模块化设计
- 置换操作统一由permute()处理
- Feistel网络独立为函数
- 子密钥生成与主算法分离
- 算法准确性
- 严格遵循DES标准文档的置换表定义
- 正确处理循环左移和密钥逆序
- 精确实现S盒查表逻辑
五、实验结果验证
加密-解密一致性
当使用相同密钥时:
加密结果 → 解密 → 恢复原始明文
验证:测试用例中解密结果与原始明文一致弱密钥特性
全01交替密钥的二次加密结果:
E(K,E(K,M)) = M
验证:测试结果符合预期
该实现完整展现了DES算法的核心机制,可用于教学演示和算法分析。通过修改测试用例,可以进一步研究DES的雪崩效应、密钥依赖性等密码学特性。
非对称加密算法RSA实现
1 | import math |
以下是关于RSA加密算法及其代码实现的详细解析:
一、RSA算法原理
1. 密钥生成流程
选择两个大素数
- 选取两个互不相同的质数 p 和 q(示例中使用 p=885320963, q=238855417)
- 代码通过
is_prime()函数验证素数性
计算模数和欧拉函数
- 模数:
n = p * q(公开参数) - 欧拉函数:
φ(n) = (p-1)*(q-1)(保密参数)
- 模数:
选择公钥指数 e
- 要求:
1 < e < φ(n)且gcd(e, φ(n)) = 1 - 代码优先选择常用值 65537(安全且计算高效),其次尝试 17/5/3,最后遍历查找
- 要求:
计算私钥指数 d
- 要求:
d ≡ e⁻¹ mod φ(n),即满足(e*d) % φ(n) = 1 - 代码使用
pow(e, -1, phi)快速计算模逆元
- 要求:
2. 加解密过程
- 加密:
c ≡ m^e mod n(使用公钥 (n,e)) - 解密:
m ≡ c^d mod n(使用私钥 (n,d))
二、代码模块解析
1. 素数检测函数
1 | def is_prime(num): |
- 功能:判断数字是否为素数
- 特点:
- 时间复杂度:O(√n)(适合教学演示)
- 实际工程中应使用Miller-Rabin等概率性检测算法
2. 公钥指数选择
1 | def find_e(phi): |
- 设计逻辑:
- 优先选择常用公钥指数(65537在安全与效率间取得平衡)
- 次优选择小素数加速加密计算
- 最后遍历保证总能找到合适指数
3. 密钥生成核心
1 | def rsa_key_generation(p, q): |
- 关键步骤:
- 输入验证确保p,q为素数
- 使用Python内置的
pow()函数快速计算模逆元 - 返回格式:公钥(n,e) 与 私钥(n,d)
4. 加解密函数
1 | def encrypt(m, public_key): |
- 数学基础:欧拉定理保证
m^(kφ(n)+1) ≡ m mod n - 限制条件:明文必须满足
m < n - 实际应用:需配合OAEP等填充方案处理长文本
三、示例测试分析
1. 输入参数
1 | p = 885320963 |
2. 密钥生成结果
1 | 公钥 (n, e): (211463707796205371, 65537) |
n计算验证:
885320963 * 238855417 = 211,463,707,796,205,371
与输出一致d验证:
(65537 * 107827558183622753) % φ(n) = 1
可通过模运算验证
3. 加解密过程
1 | 密文: 15943230000000001 |
- 加密验证:
65^65537 mod n = 15943230000000001 - 解密验证:
15943230000000001^d mod n = 65
四、算法安全性分析
依赖的数学难题:
- 大整数分解问题:已知n=p*q,难以分解出p和q
参数选择要求:
- p和q应为安全素数(示例参数过小,仅用于演示)
- 实际应用要求n长度≥2048位
常见攻击防御:
- 选择p和q长度相近但差值较大
- 使用随机填充方案防止低指数攻击
五、代码优化方向
大数处理:
- 添加对字符串消息的编解码支持
- 实现分段加密处理长文本
性能优化:
- 使用快速幂算法优化模幂运算
- 实现蒙哥马利模乘加速计算
安全性增强:
- 添加PKCS#1 v1.5或OAEP填充方案
- 支持CRT(中国剩余定理)加速解密
六、实验现象解释
弱密钥现象
当选择特殊参数时(如p=17, q=17),会导致加密失效
代码通过is_prime()检测避免了重复素数明文限制
示例中若选择m = n会触发ValueError
实际应用中需通过填充保证m < n
该实现完整展现了RSA的核心数学原理,可用于教学演示和算法分析。通过修改素数生成方法,可以进一步研究RSA算法的实际应用场景和安全性特征。
签名
1 | from Crypto.Cipher import AES |
下面我从整体流程到代码细节,分三部分给你讲解——即便你是密码小白,也能跟着思路一步步弄懂:
一、整体加密+签名流程概述
本实验演示的是一种“带保密性(Confidentiality)+带签名(Authenticity)”的混合加密方案,大致分三步:
数字签名(Authentication)
- 对明文
M先做 哈希(SHA‑256),得到消息摘要H = SHA256(M) - 用发送方的 RSA 私钥对
H进行 PKCS#1 v1.5 签名,得到签名S
- 对明文
对称加密(Confidentiality)
- 生成一次性随机 AES 密钥
K和初始向量IV - 用 AES-CBC 模式对原文
M进行加密,得到密文C = AES_CBC_Enc(K, IV, M)
- 生成一次性随机 AES 密钥
密钥封装(Key Encapsulation)
- (可选/示例中未实现)用接收方 RSA 公钥将对称密钥
K加密,得到E = RSA_Encrypt(Pub_recipient, K) - 最后将三部分打包发送给接收方:
{ E, IV, C, S }
- (可选/示例中未实现)用接收方 RSA 公钥将对称密钥
接收方收到后,按反向步骤依次:
- RSA 解密拿到对称密钥
K - 用
K, IV解 AES,得到明文M′ - 对
M′再做 SHA‑256,得到H′,用发送方公钥验证H′是否匹配签名S
这样既保证了内容的保密性,又保证了发送者身份的不可否认性和完整性。
二、代码流程详解
你给出的代码示例,主要实现了上面第 1、2 步(签名 + 对称加密 + 解密 + 验签),我们分块看:
1 | from Crypto.Cipher import AES |
- 引入了 PyCryptodome 库的 RSA, AES, SHA256, PKCS#1 v1.5 签名 以及 随机数、填充 工具。
1. 哈希函数
1 | def sha256_hash(data: str): |
- 功能:对字符串
data做 SHA‑256,返回一个Hash对象,供签名或验证使用。
2. RSA 签名/验签
1 | def rsa_sign(private_key, hash_obj): |
- 签名:用私钥对
hash_obj进行 PKCS#1 v1.5 签名,返回原始字节串signature。 - 验签:用公钥验证签名,若匹配则返回
True,否则抛异常并返回False。
3. AES-CBC 加解密
1 | def aes_encrypt(plaintext: bytes, key: bytes, iv: bytes) -> bytes: |
- 加密:
- 用
key, iv构造 AES-CBC 对象 - 对明文
plaintext先做 PKCS#7 填充(块长 16 字节),再加密
- 用
- 解密:反向解密并去除填充
4. 主流程
1 | if __name__ == '__main__': |
- 生成 RSA 密钥对
- 签名:对
"Hey"的 SHA‑256 做签名 - 拼接:为了简化,把签名字节直接追加到明文后面
- AES-CBC 加密:对拼接后的数据加密
- AES-CBC 解密
- 分离出明文和签名,再次做 SHA‑256,验签
注意:代码中并没有把
aes_key用 RSA 公钥加密;在真实场景下,应当将aes_key也封装进消息里,保证对称密钥的机密性。
三、完整示例:加上“密钥封装”的改进
下面给出一个更完整的示例,加入“用接收方 RSA 公钥加密 AES 密钥”这一步:
1 | from Crypto.Cipher import AES, PKCS1_OAEP |
这样就完成了:
- 签名(防篡改+身份认证)
- 对称加密(高效保密)
- 密钥封装(保证对称密钥的机密性)
小结
- SHA‑256 负责生成消息摘要。
- RSA 私钥签名 + 公钥验签 保证消息未被篡改且确实来自发送方。
- AES-CBC 高效地加密大段数据。
- RSA-OAEP(或 PKCS#1 v1.5)封装对称密钥,既保密又兼容公钥基础设施。
这套混合加密+签名方案,正是很多安全协议(如 TLS)在应用层面使用的基本思路。希望这个分步详解,能让你对每一步的“为什么要这样做”和“代码如何实现”都清晰明了!如果还有任何疑问,随时提~





